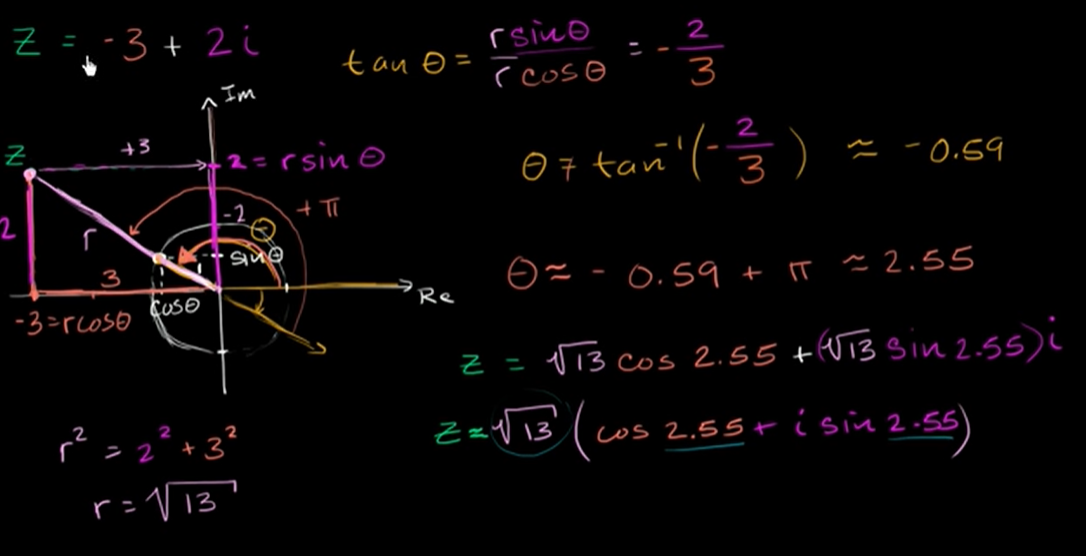Math

• Linear Algebra MIT MIT
• Math Deep University of Penn
• Online math textbooks
• Matrix cookbook
• Pre calculus and College algebra
• Algebra Derek banras
• Polyhedra
• Koebe polyhedra
• Geometry junkyard polyhedra

• Vectors
• Trignometry
  • Sine and Cosine
    • Sine and cosine visually explained
    • The “co” in trigonometric functions stands for “complement”. The complement of an angle is the angle subtracted from a right angle. For example, the complement of 40 degrees is 50 degrees. The “cosine” is the “sine of the complement”. This means that sin40∘=cos50∘sin⁡40∘=cos⁡50∘ ** Or, in general: **sin(90∘−x)=cosxsin⁡(90∘−x)=cos⁡x
    • Since the two non-right angles of a right triangle are complementary, this means that the sine of one angle in a right triangle will be the cosine of the other. If you memorized all your triangle ratios, then any trig function can be converted to it’s complement function by swapping “adjacent” and “opposite”. For example,
    • 
• Calculus
• Pre Calculus

• Number system
  • Integers, from the Latin word which means whole are numbers without fractions, both positive and negative.
  • Natural numbers or Counting numbers are all natural numbers with positive integers starting from one.
  • **Whole numbers **are natural numbers starting from 0.
  • Real numbers are numbers that include both rational and irrational numbers.
  • Rational Number. Any number that can be represented as a factor of two numbers is a Rational number P/Q. Rational numbers are real finite numbers or decimals with repeating values.
  • **Irrational numbers **are Real numbers that are infinite and never repeating Eg- Pi.
  • Prime Numbers are natural numbers that are only divisible by two numbers, themselves and one. Prime numbers are like the atoms of the number systems, they cannot be broken down into factors. The number one is divisible by only one number, 1 hence it is not prime. 2 is the only even prime number.
  • Composite numbers have more than 2 factors.
  • Imaginary Numbers
    • There is no real number solution to the equation x^2=-1, because it is impossible to square a real number and get a negative number! The solution to this exists in the Complex number system
    • The backbone of this number system is the imaginary unit i with the definition** i^2 = -1**. By taking mutliples of this number we can create many imaginary numbers.
    • 
    • 
    • i as the principle square root of -1
      • 
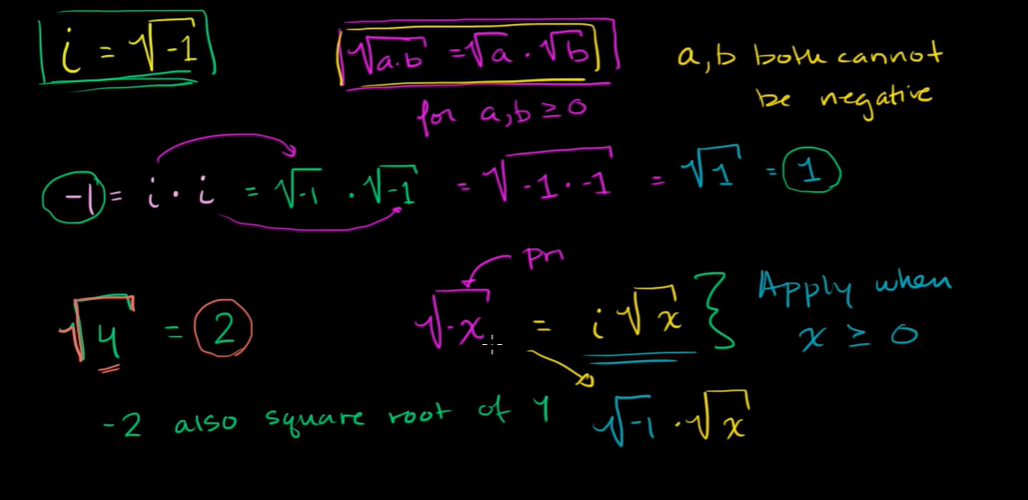
      • When we up i as the sqrt of -1 the fault in the logic is using the sqrt(a.b), as this is only true when a,b >0 if both a and b are negative then it is no longer valid.
  • Complex Numbers
    • A complex number has both real and imaginary parts, They are numbers which can be written in the form a+bi where a and b are real numbers. they are represented in the complex plane with the real part on the x-axis and the imaginary part on the Y-axis.
    • 
    • 
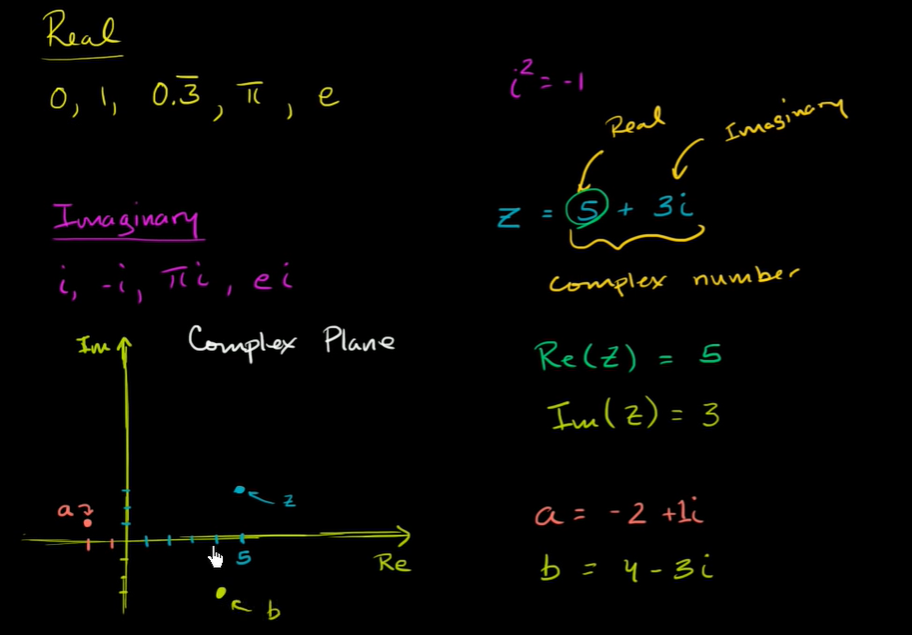
    • The complex plane or the Argand Diagram
      • 
      • Geometric representation of z and its conjugate z̅ in the complex plane. The distance along the light blue line from the origin to the point z is the modulus or absolute value of z. The angle φ is the argument of z.
      • 
    • Arithmetic operations on Complex numbers
      • 
      • 
    • Conjugate of complex number
      • For a complex number a+bi the conjugate of the number z̅ is a-bi.
      • *Z + z̅ = 2 Re(Z) **
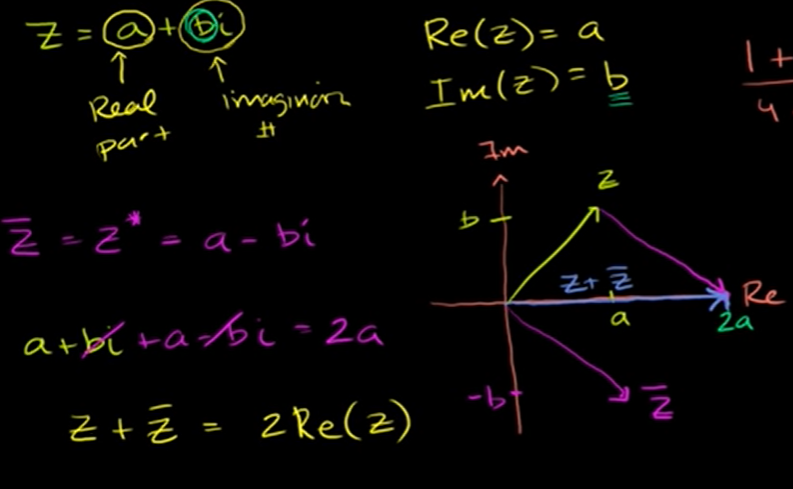
      • This is useful when simplifying complex numbers like in the division of complex numbers, if you multiply the numerator and the denominator with the conjugate of the denominator then you can convert the denominator into a real number as a number multiplied by its conjugate is a real number.
      • 
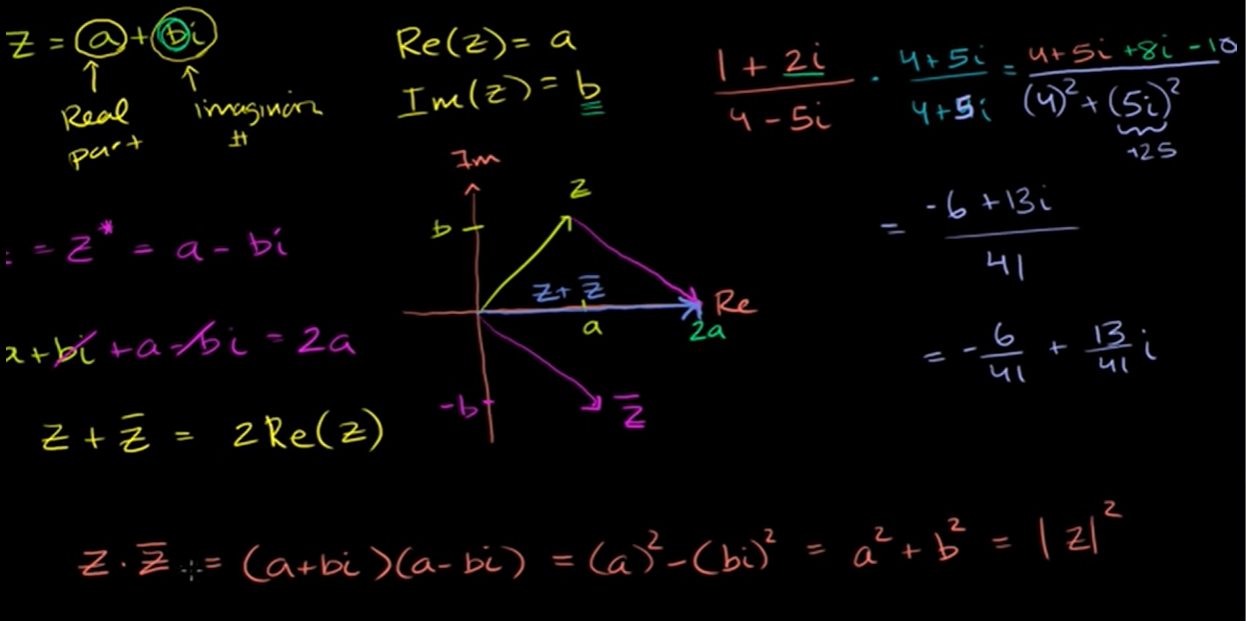
    • Division of Complex numbers
      • 
    • Expressing sum of Squares
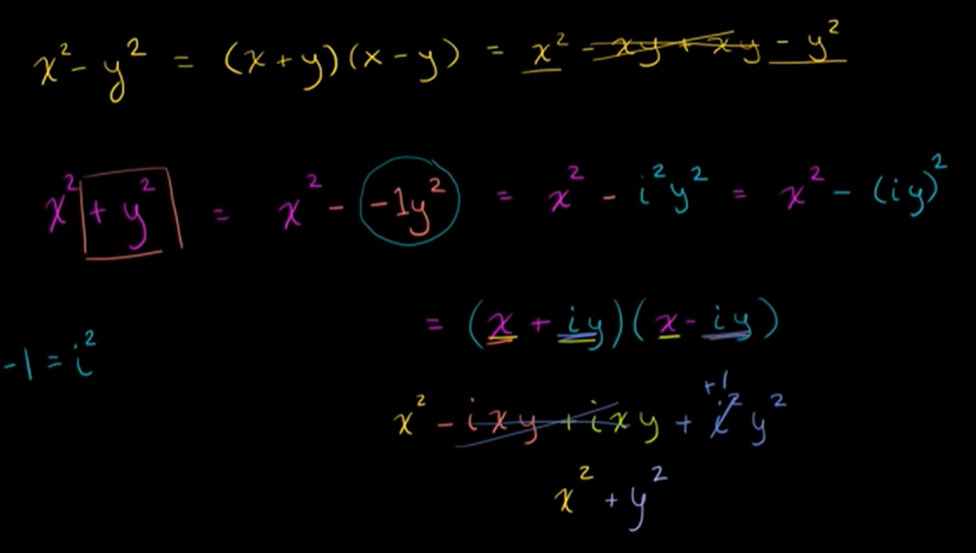
      • The difference of squares can be expressed as a multiplication of the addition and subtration of the same terms but the sum of squares can be expressed as a difference of squared by introducing the imaginary unit.
    • The Absolute value and argument of complex numbers
      • The absolute value is the distance of the point from the origin in the complex plane. Its given by the Pythagoras therorem.
      • 
      • 
      • 
      • 
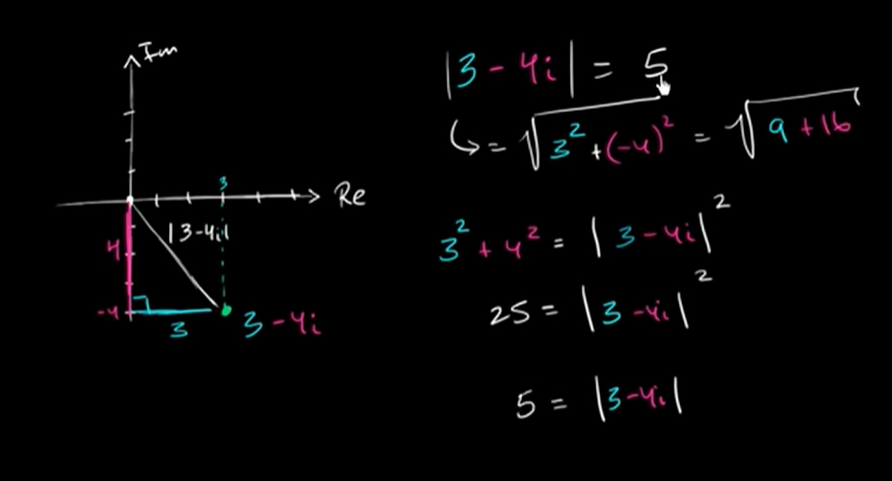
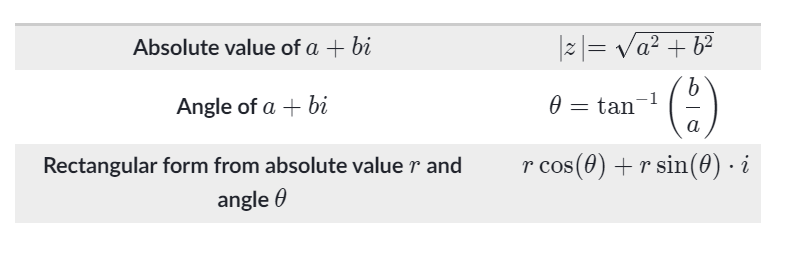
    • Polar form of complex numbers
      • 

tags: #Math

tags: #Math #Khan Academy

Math

tags:Math

• Essence of Calculus 3Blue1Brown learning
• Multi variable Calculus Khan Academy, look to learn basic math, explore other courses. learning
• Essence of Linear Algebra 3Blue1Brown learning watch